simplificacion
de radicales.
HAY
2 TIPOS DE SIMPLIFICACION DE RADICALES:
-
SIMPLIFICACION DE RADICALES
CUYOS RADICANDOS SON NUMEROS.
-
SIMPLIFICACION DE RADICALES CUYOS
RADICANDOS SON VARIABLES.
SIMPLIFICACION
DE RADICALES CON NUMEROS.
Los pasos para llevar a cabo
la realización de simplificación de radicales con numeros
es con los siguientes pasos:
-
Escribir el radicando como el producto
de dos números, uno de los cuales sea el mayor número que
es potencia perfercta para el índice dado.
-
Utilice la regla del producto para
escribir la expresión como producto de raíces. (Regla)
-
Determine las raíces de los
números que son potencias perfectas.
ejemplo:
simplifique 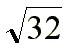
solucion:
como estamos evaluando
una raiz cuadrada, buscamos el maximo cuadrado perfecto que divida a 32.
el maximo cuadrado perfecto que divide a 32, o es factor de 32 es
16.
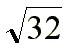 *
* 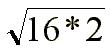 =
= 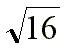
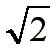 =
= 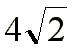
simplificacion
de radicales con variables.
Los pasos
para llevar a cabo la realizacion de simplificacion de radicales con variables
es con los siguientes pasos:
-
Escriba cada variable como el producto
de 2 factores, uno de los cuales sea la máxima potencia perfecta
de la variable para el índice dado.
-
Utilice la regla del producto para
escribir la expresión radical como un producto de radicales. Coloque
todas las potencias perfectas bajo el mismo radical.
-
Determine las raíces de todas
las potencias perfectas.
El maximo cuadrado perfecto de
x9 es x8 .
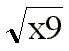 =
= 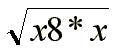 =
= 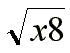
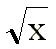 = x4
= x4 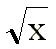
*
=
=
=
=
= x4